A continuation scheme for RELU activation functions

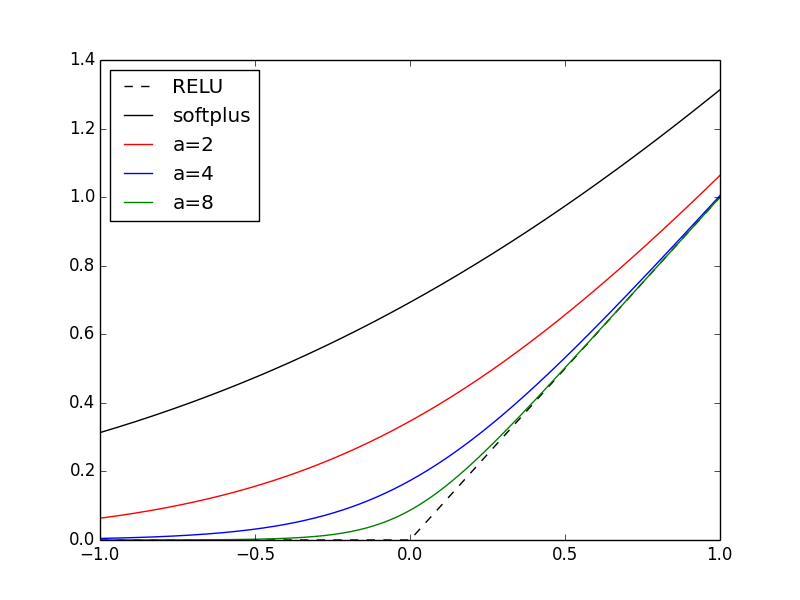
26 Nov 2018

One of the most popular activation function nowadays is the REctified Linear Unit (RELU), defined by $f(x) = \max(0,x)$. One of the first obvious criticism is its non-differentiability at the origin. A smooth approximation is the softplus function, $f(x) = log(1 + e^x)$. However, the use of softplus is discouraged by deep learning experts. I’m wondering if a continuation scheme on the softplus could help during training. Instead of softplus, we could use a “smooth RELU” defined as

\[f_\alpha(x) = \frac1{\alpha} log(1 + e^{\alpha x})\]

And starting with $\alpha = 1$, i.e., the softplus function, we increase $\alpha$ after each epoch with the effect of smoothly converging toward RELU. In the plot below, I show RELU, softplus, and 3 examples of smooth RELUs for $\alpha=2,4,8$.

[ deeplearning  relu  activation  optimization  ]